Elliptic curve cryptography

Andrei Zhozhin
| 9 minutes
Elliptic curves or ECC (Elliptic Curve Cryptographic) or ECDSA (Elliptic Curve Digital Signature Algorithm) are already used in blockchain and to protect HTTP traffic as they have a compact size and much larger private keyspace than older algorithms like RSA (Rivest–Shamir–Adleman). As ECC provides the same level of security with a much shorter key length it is much more preferable for low power devices and limited storage (Internet of things and mobile devices). In SSL/TLS ECC reduces time to perform SSL/TLS handshake thus reducing overall load time. Regarding computation complexity on high levels of security (>128 bit) RSA performance decline dramatically (with RSA keys longer than 3072) while ECC still performing very well. At the same time, RSA is very mature and widely adopted as RSA was standardized in 1994 (patent expired in 2000), and the algorithm itself was invented in 1977. Contrary ECC entered wide use in 2005.
| Metric | RSA | ECDSA |
|---|---|---|
| Adoption | x | |
| Maturity | x | |
| Key size | x | |
| Performance | x (short keys) | x (long keys) |
| Scaling | x |
Table with key length comparison between RSA and ECC
| Security (In Bits) | RSA Key Length Required (In Bits) | ECC Key Length Required (In Bits) |
|---|---|---|
| 80 | 1024 | 160-223 |
| 112 | 2048 | 224-255 |
| 128 | 3072 | 256-383 |
| 192 | 7680 | 384-511 |
| 256 | 15360 | 512+ |
Please note that after 128 bits of security RSA key growing very fast.
Elliptical curves
Elliptical curves could be defined as the following equation:
y^2 = x^3 + a*x + b
It could be defined as the real field or finite field. In the case of the finite field, all numbers are integers which allow quick computational operations.
Shapes of elliptic curves
The following elliptic curves are defined in a real field. There are many curves in use, some of them are recommended for secure implementation, some of them are not. Here is a list of curves and their coefficients for comparison.

Secp256k1 curve
For Bitcoin and Etherium the same elliptic curve is used - secp256k1 with a=0 and b=7.
So the elliptic curve equation looks like that: y^2 = x^3 + 7.
We have our elliptic curve defined over integer field so it would be:
y^2 mod p = (x^3 + 7) mod p
The mod p - (modulo prime number p) indicates that the curve is over the finite field of prime order p (Fp).
Where p = 2^256-2^32-2^9-2^8-2^7-2^6-2^4-1 or in hex 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
So even if the elliptic curve formula looks simple it is calculated for points in a very big field.
Elliptic curve over real field (y^2 = x^3 + 7):

Elliptic curve over a finite field of prime order 17 y^2 = (x^3 + 7) mod 17 (it is not possible to visualize real point distribution for p):

As you can see finite field dots have still preserved some symmetry over the horizontal axis.
Before we go to private and public keys we need to understand operations that we can do with points on elliptic curves.
Elliptic curve arithmetic operations
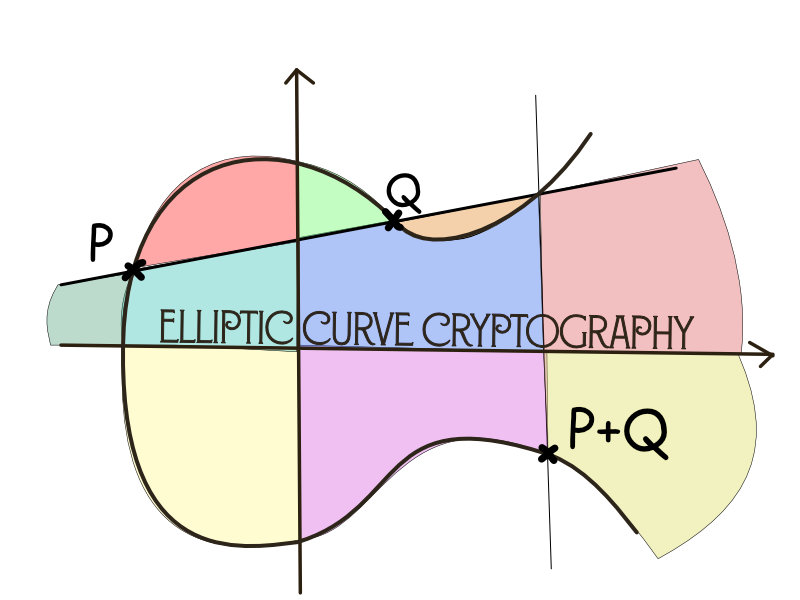
Elliptic curve addition is defined as R = P + Q, when all points belong to the same curve.
There is a geometric interpretation of addition:

If we draw a line from P to Q and find the intersection with curve we would get -R point, finding the opposite point over the x-axis would give us R.
If we have addition then we can implement multiplication k * P = P + P + ... + P (k times)
All operations over elliptic curves (source: Wikipedia):

Please note that this shape of the curve with a=-1 and b=1 (y^2 = x^3 - x + 1)
Operations: 1 - addition, 2, 4- doubling, 4 - negation
If we apply several operations one after another it could be depicted as the following (Visualization for curve y^2 = x^3 - x + 1):

In we look at the finite field then the same operations could be visualized like the following (coordinates overlap), this visualization for curve y^2 = x^3 - x + 1 using prime order of 97:

Private key generation
A private key is a single number selected from the range [0, n-1] where n = 2^256.
So Etherium private keyspace is 2^256, to give you an idea of how big it is 2^256 ~ 1.158 * 10^77. For comparison, the visible universe is estimated to contain between 10^78 and 10^82 atoms.
If you pick a number randomly from this space there is practically impossible to guess it.
Let’s generate a private key using python (using ecdsa library)
import ecdsa
sk = ecdsa.SigningKey.generate(curve=ecdsa.SECP256k1)
private_key = sk.to_string().hex()
print(private_key)
Example output (if you would run the code above you would get another result)
f9e6a7cb98b65206b21ddf094e0b0994d4ca79f1db769ef6b83dd2a513d69ffe
Public key
The public key could be derived from the private key using the following formula:
K = k * G
Where k - private key and G - generator point is defined as constant for every elliptical curve, * - is the elliptical curve multiplication operator.
Because this operation is performed over finite field multiplication is not reversible, thus if you have a public key and generator point it is not possible to divide public key K value by generator point G value to derive k. Because multiplication is not reversible you can safely share the public key with the world.
Generator point G:
Gx=55066263022277343669578718895168534326250603453777594175500187360389116729240
Gy=32670510020758816978083085130507043184471273380659243275938904335757337482424
We can check that this point belongs to the curve
(Gy**2 - Gx**3 - 7) % p # returns 0
Let’s generate private key from private
vk = sk.get_verifying_key() #this is your verification key (public key)
public_key = vk.to_string().hex()
print(public_key)
Output in hex
0634463de6107896b12c54938d9750ce5198a6fe5128f4751ab67aa8762f8659a0a015aa2138139 \
c3f585f5ce1677461ef7040ca9ba34c6b81bf589824fb9906
Now we need to extract (x,y) components from K, it is packed as follows:
[32-byte X coordinate] + [32-byte Y coordinate]
Kx = int(public_key[0:64], 16)
Ky = int(public_key[64:128], 16)
print(Kx, Ky)
Output
(2806237929897699231504706868552850600918158324309505816486094079263327094361,
72652900827049753851382310050705759837967547972600998243662342658781131544838)
And now we can validate that that point is still on the curve:
(Ky**2 - Kx**3 - 7) % p # return 0
In practice public keys have an extra prefix byte that describes a type of packaging:
| Prefix | Meaning | Length (with prefix) |
|---|---|---|
0x00 |
Point at infinity | 1 byte |
0x02 |
Compressed point with even y |
33 bytes |
0x03 |
Compressed point with odd y |
33 bytes |
0x04 |
Uncompressed point | 65 bytes |
The compressed format is using only x coordinate, but because there are two y coordinates on the curve for a single x, there are prefixes that define odd or even y should be used. Then y could be calculated as sqrt(x^3+7)
Compressed keys are two times shorted while having the same information.
So compression format:
('0x02' or '0x03') + x-coordinate (32 bytes/64 hex)
The uncompressed format looks like the following:
'0x04' + x-coordinate (32 bytes/64 hex) + y-coordinate (32 bytes/64 hex)
To get a properly formatted public key we need to add 0x04 prefix to indicate that we are using the uncompressed format:
real_public_key = '04' + public_key
Output
040634463de6107896b12c54938d9750ce5198a6fe5128f4751ab67aa8762f8659a0a015aa2138139 \
c3f585f5ce1677461ef7040ca9ba34c6b81bf589824fb9906
Etherium Address
Address in the Etherium network could also be derived from the private key: we need to calculate the Keccak256 hash from the public key, and take the last 20 bytes out of 32 bytes of hash.
Address = B[96..255](Keccak256(PublicKey(private_key)))
Let’s calculate the address using the following code
import sha3
keccak = sha3.keccak_256()
keccak.update(bytes.fromhex(public_key))
addr = keccak.digest()[-20:]
print('0x' + bytes.hex(addr)) # prefix `0x` required to get valid Etherium address
Output
0x89d2f65116a8c1eca8c7a471bf93c932f8f2c70b
We can compare it with address derivation logic in web3.py:
from web3 import Web3
web3 = Web3()
acc = web3.eth.account.privateKeyToAccount(private_key)
print(acc.address)
Output
0x89d2f65116a8c1eCa8c7a471bf93C932F8f2c70b
Both addresses matched which means our code produce correct results.
Signing
ECDSA use two numbers (integers): r and s, in addition, there is also the recovery identifier v.
Let’s say we have a message and a private key da. The signing process would be the following.
- Calculate hash of the message
e = hash(message) - Generate secure random value
k - Calculate
R = k*G, whereGis a generator point - Calculate
r = R.x % n, ifrequal to zero, goto step 2 - Calculate
s = 1/k * (e + r*da) % n, ifsequal to zero, goto step 2
Recovery identifier v is used to remove ambiguity between 4 points during verification, every value r have two Y points on the curve, and because r = R.x % n there is also possible that point might be r + n with two corresponding Y values. If you don’t have v then you need to check all 4 points until you find the one that matches the public key.
Fortunately, there is python implementation for signing:
import ecdsa
private_key = "f9e6a7cb98b65206b21ddf094e0b0994d4ca79f1db769ef6b83dd2a513d69ffe"
message = "Hello world!"
sk = ecdsa.SigningKey.from_string(bytes.fromhex(private_key), curve=ecdsa.SECP256k1)
public_key = sk.get_verifying_key()
message_bytes = str.encode(message)
sig = sk.sign(message_bytes, hashfunc=sha256)
print(f"Public key: {public_key.to_string().hex()}")
print(f"Signature : {sig.hex()}")
The output of the script above (output is formatted to fit into layout)
Public key: 0634463de6107896b12c54938d9750ce5198a6fe5128f4751ab67aa8762f8659a0a015 \
aa2138139c3f585f5ce1677461ef7040ca9ba34c6b81bf589824fb9906
Signature : ffbf419f39486dfcd057bf0fd38c67e8fb82ef338e13e49b2259baa22ff083b2c4f57c \
49ecff1e39d3c60d13bc5529bb233d9560d150b3b06f5c6806055ce91a
Our signature is standard thus it is 64 bytes/128 hex.
Signature format for standard signatures (r and s only) total 64 bytes / 128 hex:
r-value (32 bytes/64 hex) + s-value (32 bytes/64 hex)
For Etherium there is also v (27/0x1B or 28/0x1C) added at the end total 65 bytes / 130 hex:
r-value (32 bytes/64 hex) + s-value (32 bytes/64 hex) + v-value (1 byte/2 hex)
Verifying Signature
The idea of signature verification is to prove that message was not amended by someone and it is created by the person you expect (based on their public certificate)
- Calculate hash of the message to verify
e = hash(message) - Calculate point
R = (x1, y1)on the curve, wherex1 = rifv==27, orx1 = r+nifv==28 - Calculate two numbers
u1 = -z/r % nandu2 = s/r %n - Calculate point
Q = (xa, ya) = u1 x G + u2 x R
Point Q is a public key for private key that was used to sign the message. If it matches the expected public key - a signature is valid.
We are using public_key and signature from previous example
from hashlib import sha256
message = "Hello world!"
message_bytes = str.encode(message)
public_key= '0634463de6107896b12c54938d9750ce5198a6fe5128f4751ab67aa8762f8659a0a015 \
aa2138139c3f585f5ce1677461ef7040ca9ba34c6b81bf589824fb9906'
sig = 'ffbf419f39486dfcd057bf0fd38c67e8fb82ef338e13e49b2259baa22ff083b2c4f57c \
49ecff1e39d3c60d13bc5529bb233d9560d150b3b06f5c6806055ce91a'
vk_bytes = bytes.fromhex(public_key)
vk = ecdsa.VerifyingKey.from_string(vk_bytes, curve=ecdsa.SECP256k1, hashfunc=sha256)
vk.verify(bytes.fromhex(sig), message_bytes) # True
In Etherium hash calculated like the following: Keccak256("\x19Ethereum Signed Message:\n32" + Keccak256(message)) to avoid using outside of Etherium network.
Big tech and cryptography
I’ve checked several big tech companies web sites to understand the adoption of elliptic curve cryptography and here are the results:
| Company | Web site | Signature hash | Public key |
|---|---|---|---|
| https://google.com | SHA256 | ECC (256 bits)/ECDSA_P256 | |
| https://facebook.com | SHA256 | ECC (256 bits)/ECDSA_P256 | |
| Amazon | https://amazon.com | SHA256 | RSA (2048 bits) |
| Apple | https://apple.com | SHA256 | RSA (2048 bits) |
| Microsoft | https://microsoft.com | SHA256 | RSA (2048 bits) |
| https://twitter.com | SHA256 | RSA (2048 bits) |
Some of the companies already switched to ECDSA while others are still on RSA as it is still good enough.
Summary
We have looked at elliptical curves and understood how to do operations on them. We generated a private key and derived a public key using multiplication on an elliptic curve. We validated that all points we’ve got belong to the same curve. We also locked in the signing and verification process.
All this cryptographic code may look tedious, but this is fascinating that these approaches and algorithms are enabling top-level security and allow to build mind-blowing things on top of them.


